See more statistics and probability topics. Reproductive age women accurately reported their height and weight.
245 Correlation
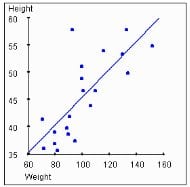
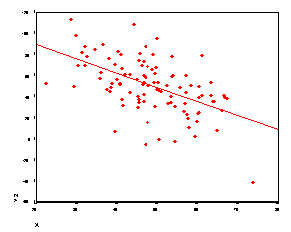
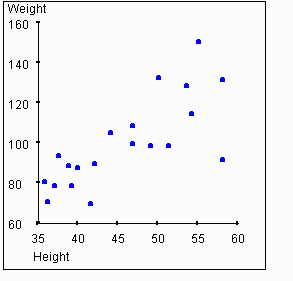
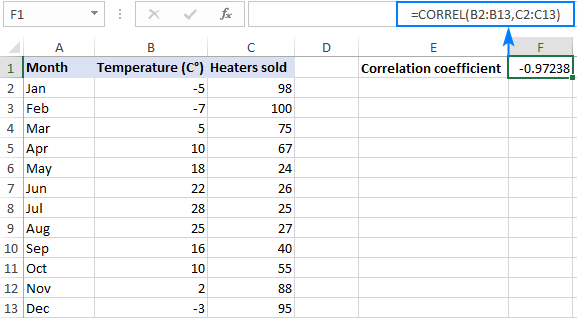
Correlation coefficient height and weight. Pearson correlation coefficient can be used to determine whether the height and the weight of the people are correlated that is if there is any relationship between height and weight of the people. Since0007 05 we can conclude that the correlation between weight and height in this example is statistically significant at alpha 05. In the first question height is measured in inches. There is a 95 chance that the confidence interval of 25027658 contains the true population correlation coefficient between height and weight of residents in this county. The pearson correlation coefficient is used to measure the strength of a linear association between two variables where the value r 1 means a perfect positive correlation and the value r 1 means a perfect negataive correlation. Self reported weight self reported height reproductive age women.
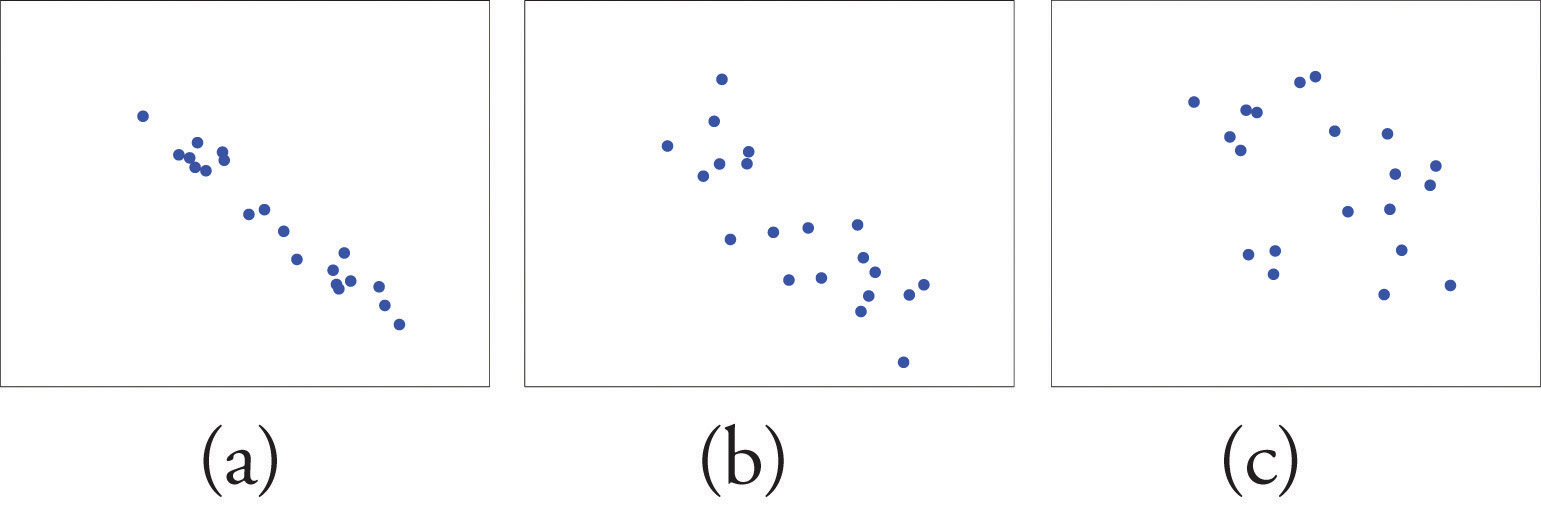
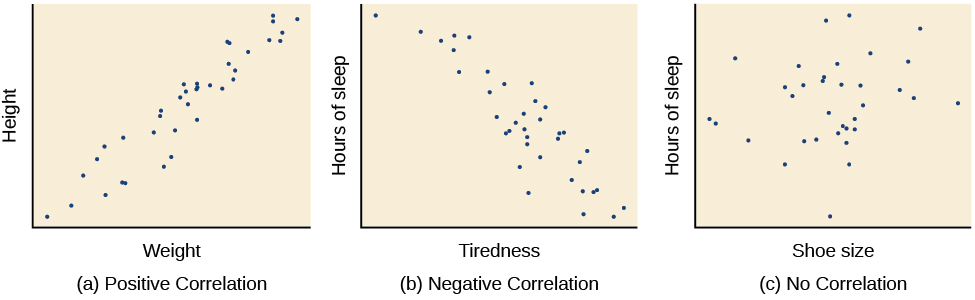
In other words a 10 increase in height is tied to a 31 increase in weight. So for example you could use this test to find out whether peoples height and weight are correlated they will be the taller people are the heavier theyre likely to be. Theres a strong correlation between height and weight. Pearsons correlation coefficient for height 096 p0001 weight 099 p0001 and bmi 099 p0001 were high. Calculate the correlation coefficient of height and weight. Make a scatterplot of height vs weight to visualize the correlation.
For a pair of variables r squared is simply the square of the pearsons correlation coefficient. Many studies have found this relationship. Another way of saying the same thing is that there is only a 5 chance that the true population correlation coefficient lies outside of the 95 confidence interval. For example squaring the height weight correlation coefficient of 0694 produces an r squared of 0482 or 482. Find the mean standard deviation and 95 confidence interval for both variables. Suppose you converted the data to feet.
For example consider a data of the height and the weights of people. In other words height explains about half the variability of weight in preteen girls. In general weight increases as the cube of the increase in height.
Gallery of Correlation Coefficient Height And Weight
/TC_3126228-how-to-calculate-the-correlation-coefficient-5aabeb313de423003610ee40.png)
