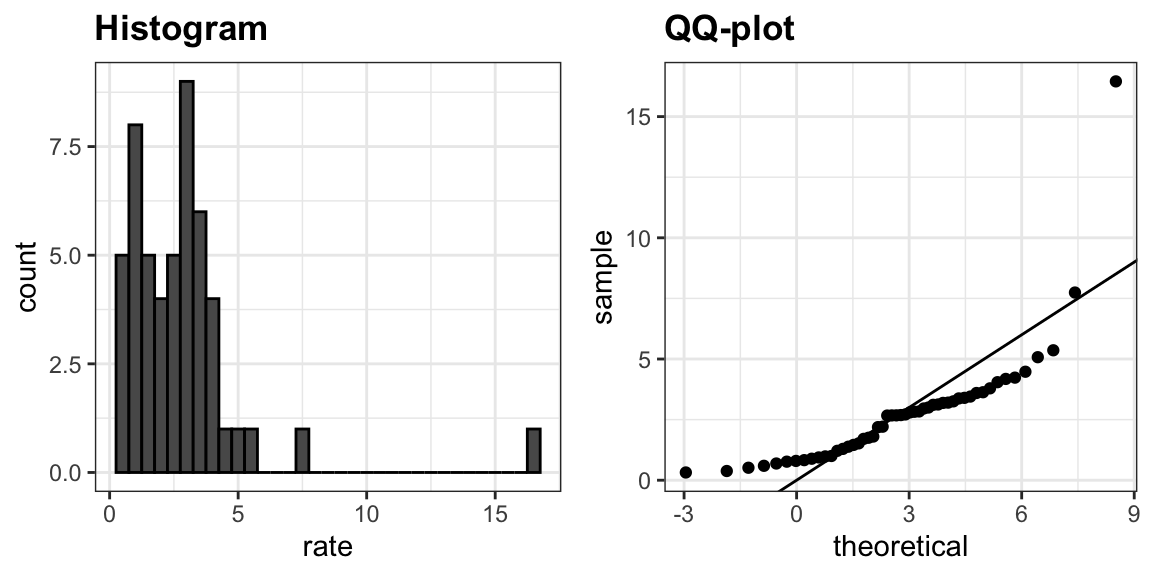
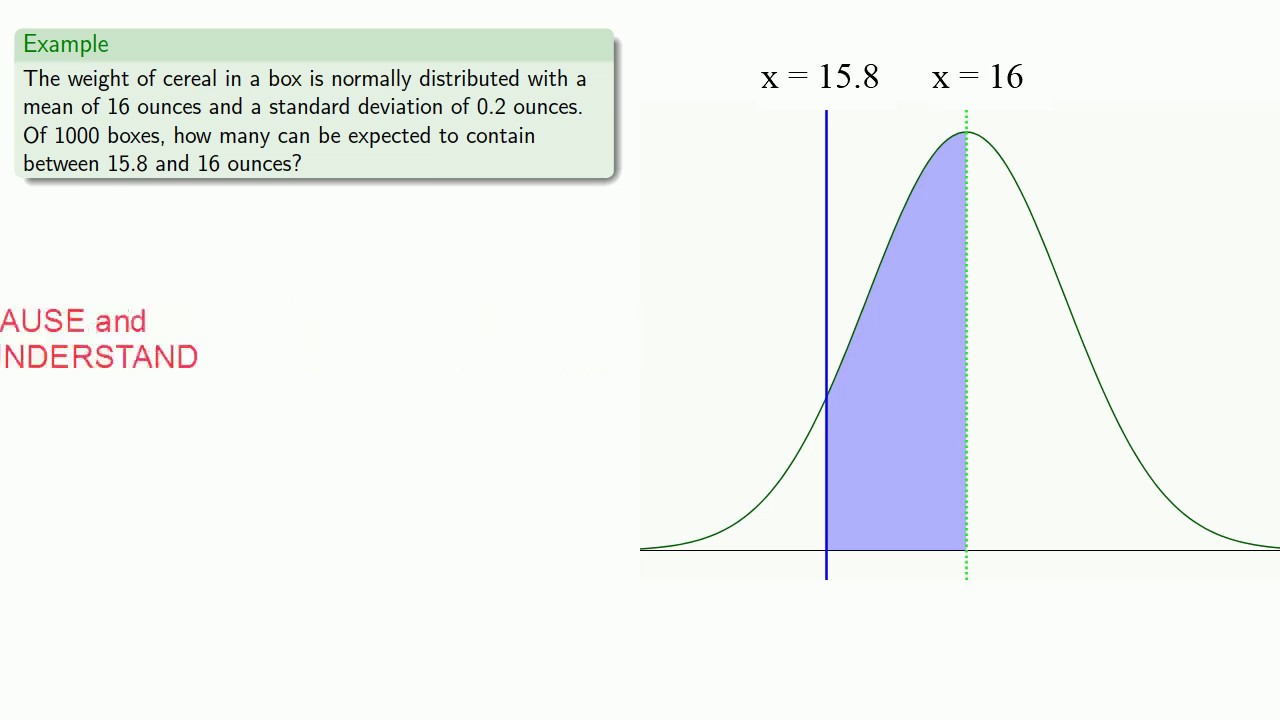
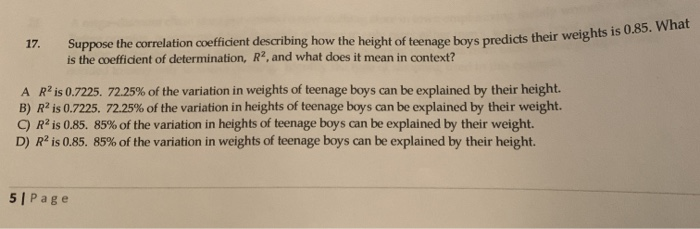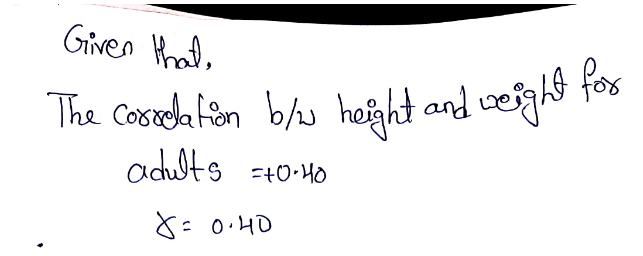Spearman correlation suppose that the correlation between height and weight for adults is 040. In general weight increases as the cube of the increase in height.
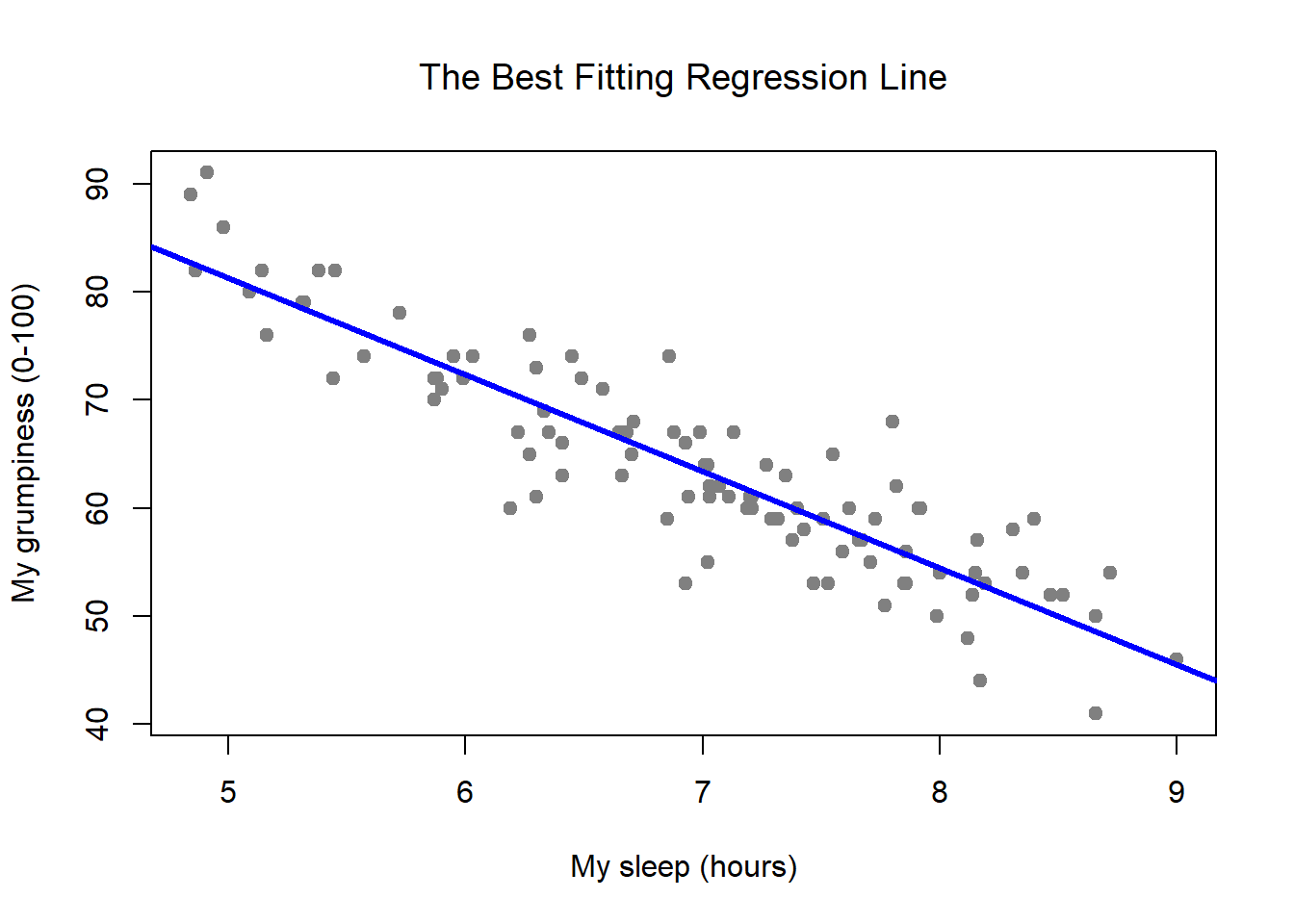
Chapter 15 Linear Regression Learning Statistics With R A
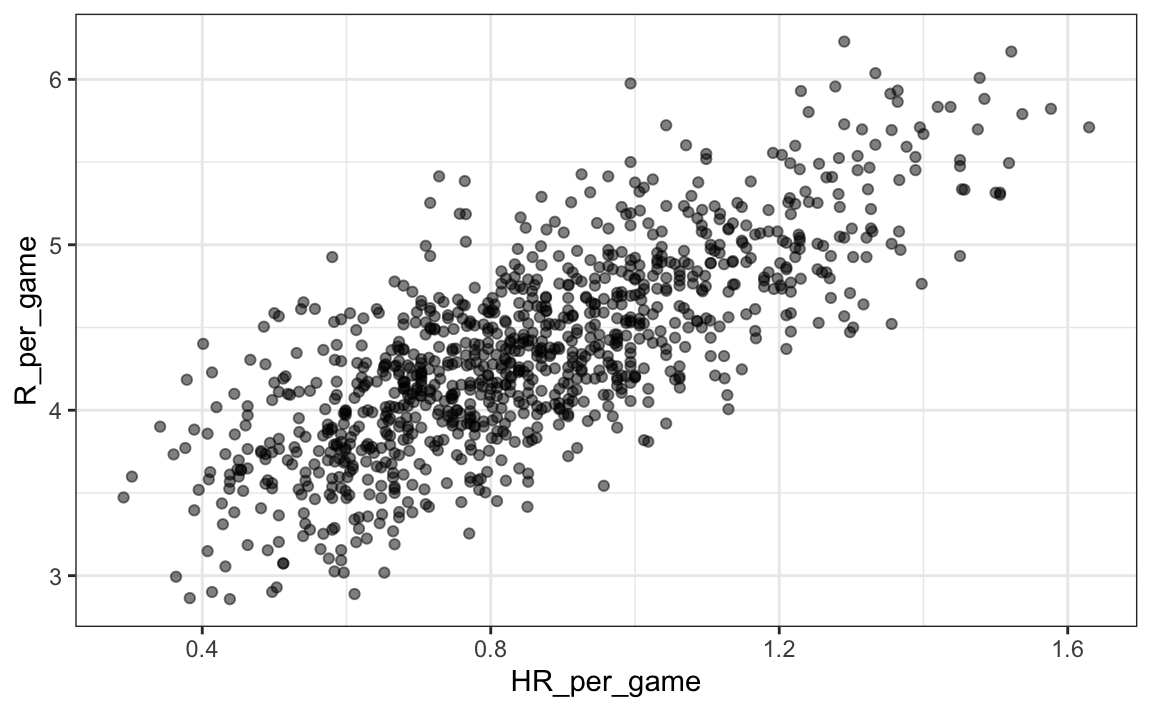
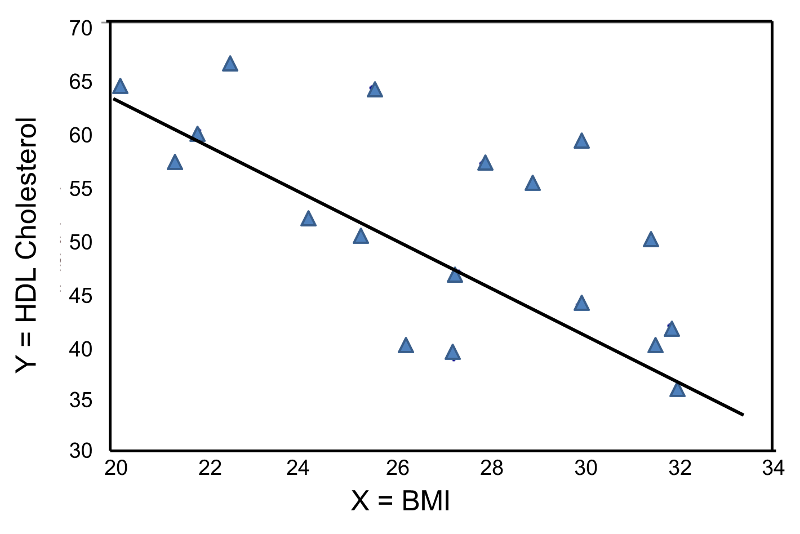
Suppose the correlation between height and weight. Given that correlation between height and weight for adults is 040. Suppose the correlation between height and weight for adults is 080. Take a look at the correlation between the height and weight data 0694. A 80 b 64 c 100 80 20 d 40. What proportion or percent of the variability in weight can be explained by the relationship with height hint. We need to find the proportion of the variability in weight that can be explained by the relationship with height.
What is a value of the coefficient of determination for this r. In other words a 10 increase in height is tied to a 31 increase in weight. Which correlation should be used to measure the relationship between these two variables. What proportion or percent of the variability in weight can be explained by the relationship with height1 802 643 100 80204 40please show how you got answer submitted10 years ago. Height in centimeters minus 100. Theres a strong correlation between height and weight.
So r 040. It takes into account the correlation between a persons height weight body type and age. What proportion or percent of the variability in weight can be explained by the relationship with height. Suppose the correlation between height and weight for adults is 080. The coefficient of determination correlation coefficient2 r2 0402 016. Suppose the correlation between height.
We are given the correlation between height and weight for adults is 040. The correlation coefficient should accurately reflect the strength of the relationship. Height in centimeters minus 110. Its not a very strong relationship but it accurately represents our data. For people above 40. An accurate representation is the best case scenario for using a statistic to describe an entire dataset.
A100 80 20. Coefficient of determination is nothing but the proportion of variability in dependent variable. For people under 40 the formula is as follows. Suppose the correlation between height and weight for adults is 080. What proportion or percent of the variability in weight can be explained by the relationship with height. Suppose the correlation between height and weight for adults is r 060.
Gallery of Suppose The Correlation Between Height And Weight
